在计算机和互联网技术中,文本压缩是一个非常重要的技术。玩电脑的人几乎都会应用压缩和解压缩软件来处理文档。因为它除了可以减少文档在磁盘上的空间外,还有重要的一点,就是我们可以在网络上以压缩的形式传输大量数据,使得保存和传递都更加高效。
下面将介绍二叉树的一个应用,赫夫曼树和赫夫曼编码,通过它来初步理解数据压缩的原理。
赫夫曼树的定义
先来解释几个概念:
路径长度:从树中一个结点到另一个结点之间的分支构成两个结点之间的路径,路径上的分支数目称作路径长度。
树的路径长度:从树根到每一结点的路径长度之和。
结点的带权的路径长度:从该结点到树根之间的路径长度与结点上权的乘积。
树的带权路径长度:树中所有叶子结点的带权路径长度之和。
举个“栗子”:
-
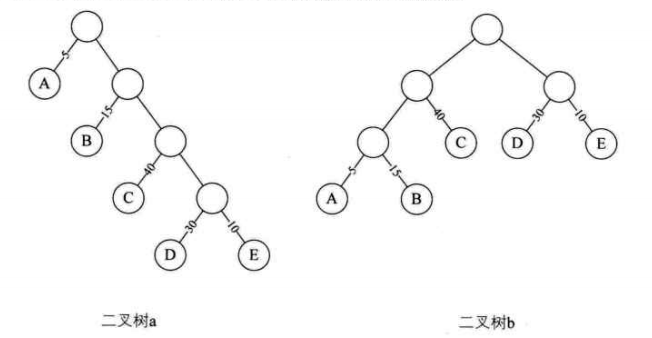
二叉树 a 中,根结点到结点 D 的路径长度就为 4;
-
二叉树 b 中,根结点到结点 D 的路径长度为 2;
-
二叉树 a 的树的路径长度就为
1+1+2+2+3+3+4+4=20; -
二叉树 b 的树的路径长度就为
1+2+3+3+2+1+2+2=16; -
二叉树 a 的带权路径长度
WPL=5*1+15*2+40*3+30*4+10*4=315 -
二叉树 b 的带权路径长度为
WPL=5*3+15*3+40*2+30*2+10*2=220
赫夫曼树:带权路径长度(WPL)最小的二叉树称作赫夫曼树。
构造赫夫曼树
构造赫夫曼树的赫夫曼算法的描述如下:
-
根据给定的 n 个权值{w1,w2,…,wn}构成 n 棵二叉树的集合 F={T1,T2,…,Tn},其中每棵二叉树 Ti 中只有一个带权为 wi 的根结点,其左右子树均为空。
-
在 F 中选取两棵根结点的权值最小的树作为左右子树构造一棵新的二叉树,且置新的二叉树的根结点的权值为其左右子树上根结点的权值之和。
-
在 F 中删除这两棵树,同时将新得到的二叉树加入 F 中。
-
重复 2 和 3 步骤,直到 F 中只含一棵树为止。这棵树便是赫夫曼树。
赫夫曼编码
编码
赫夫曼编码目的是为了解决当年远距离通信(主要是电报)的数据传输的最优化问题。
比如我们有一段文字的内容是 "BADCADFEED" 要网络传输给别人,用二进制数字来表示是很自然的想法。我们现在这段文字只有六个字母 ABCDEF,那么可以用相应的二进制数据表示,如下所示:
| 字母 | A | B | C | D | E | F |
|---|---|---|---|---|---|---|
| 二进制字符 | 000 | 001 | 010 | 011 | 100 | 101 |
这样真正传输的数据就是编码后的 001 000 011 010 000 011 101 100 100 011(空格只是为了便于显示),对方接收时可以按照 3 位一分来译码。如果一篇文章很长,这样的二进制串也将非常可怕。而且事实上,不管是英文、中文或是其他语言,字母或汉字的出现频率是不相同的,比如英语中的几个元音字母 a e i o u,中文中的的 了 有 在等汉字都是频率极高。
假设六个字母的频率为 A 27, B 8, C 15, D 15, E 30, F 5,合起来正好是 100%。那就意味着,我们完全可以重新按照赫夫曼树来规划它们。
下图中,左图为构造赫夫曼树的过程的权值显示,右图为将权值左分支改为 0,右分支改为 1 后的赫夫曼树。
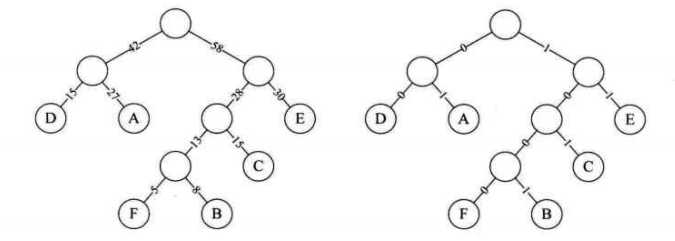
此时,我们对这 6 个字母用其从树根到叶子所经过路径的 0 或 1 来编码,如下表所示:
| 字母 | A | B | C | D | E | F |
|---|---|---|---|---|---|---|
| 二进制字符 | 01 | 1001 | 101 | 00 | 11 | 1000 |
我们将文字内容为 BADCADFEED 再次编码,对比可以看到结果串变小了。
-
原编码二进制串:001 000 011 010 000 011 101 100 100 011 (共 30 个字符)
-
新编码二进制串:1001 01 00 101 01 00 1000 11 11 00 (共 25 个字符)
也就是说,数据被压缩了,节省了大约 (30-25)/30 大约 17% 的存储或传输成本。随着字符的增加和多字符权重的不同,这种压缩会更加显出其优势。
解码
当我们接收到 1001 01 00 101 01 00 1000 11 11 00 这样压缩过的新编码时,应该如何把它解码出来呢?
编码中非 0 即 1,长短不等的话其实是很容易混淆的,所以若要设计长短不等的编码,则必须是任一字符的编码都不是另一字符的编码的前缀,这种编码叫做前缀编码。
仔细观察会发现,上表中的编码就不存在容易与 1001、1000 混淆的 “10” 和 “100” 编码。
可仅仅是这样不足以让我们去方便地解码,因此在解码时,还是要用到赫夫曼树,即发送方和接收方必须要约定好同样的赫夫曼编码规则。
当我们接收到 1001 01 00 101 01 00 1000 11 11 00 时,由约定好的赫夫曼树可知,1001 得到第一个字母是 B,接下来 01 意味着第二个字符是 A,如下图所示,其余的也相应的可以得到,从而成功解码。
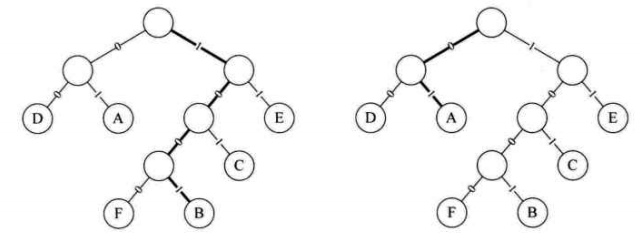
总结
一般地,设需要编码的字符集为 {d1,d2,…,dn},各个字符在电文中出现的次数或频率集合为 {w1,w2,…,wn},以 d1,d2,…,dn 作为叶子结点,以 w1,w2,…wn 作为相应叶子节点的权值来构造一个赫夫曼树。规定赫夫曼树的左分支代表 0,右分支代表 1,则从根结点到叶子节点所经过的路径分支组成的 0 和 1 的序列便为该结点对应字符的编码,这就是赫夫曼编码。